Fractions Teaching Material
Instruction
A fraction is simply a part of a whole thing. The example below is of a circle divided into four pieces. Each segment represents 1/4 of the circle.

In each of the circles below, the same area is represented, but the area is divided into different numbers of equal parts.

This diagram demonstrates that the fractions 1/2, 2/4 and 4/8 represent the same quantity.

The fractions 1/3, 2/6 and 3/9 are equivalent. You can determine fractions of equivalent value by multiplying both the numerator and the denominator of the fraction by the same number.
| 1 | x | 7 | = | 7 | thus | 7 | = | 1 |
| 3 | x | 7 | 21 | 21 | 3 |
A similar rule holds when dividing the numerators and denominators of fractions. This is necessary to reduce fractions to their lowest form.
| 5 divided by 5 | = | 1 |
| 15 divided by 5 | 3 |
Improper Fractions
When a fraction has a larger numerator than denominator then the fraction is larger than one. The diagram below illustrates an example of improper fractions.
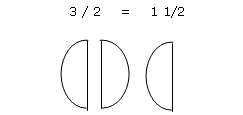
Adding and Subtracting Fractions
Whenever you are adding or subtracting fractions, you have to ensure that the denominators of the fractions are the same. For example:
| 1 | + | 6 | does not equal | 7 |
| 2 | 8 | 10 |
By multiplying both the denominator and the numerator of 1/2 by 4, you will be able to add the fractions together. 1/2 becomes 4/8.
| 4 | + | 6 | = | 10 |
| 8 | 8 | 8 |
When you are adding and subtracting fractions, you also maintain the same denominator, and add or subtract the numerator.
| 3 | - | 1 | = | 2 | = | 1 |
| 4 | 4 | 4 | 2 |
| 3 | + | 12 | = | 15 | = | 5 |
| 18 | 18 | 18 | 6 |
| 5 | - | 3 | = | 2 | = | 1 |
| 10 | 10 | 10 | 5 |
| 7 | + | 5 | = | 12 | = | 1 | 4 | = | 1 | 1 |
| 8 | 8 | 8 | 8 | 2 |
Peer Support
If you are having difficulty with the subject matter, there is always a great deal of support available to you from other members through the Forum. Simply do a search for the material you need help with (math, algebra, integers, etc.) Members are very supportive and helpful. Don't hesitate to post any questions, or provide answers to others seeking assistance.
Adding and Subtracting Fractions Practice Tests
Work through the following tests to make sure you are comfortable with the material.




Multiplying Fractions
When multiplying fractions, there is no need to find a common denominator. Simply multiply the two top numbers and then multiply the two bottom numbers. Multiplying two fractions together (other than improper) will result in a fraction that is smaller than the original numbers.
| 4 | x | 3 | = | 12 | = | 3 |
| 5 | 4 | 20 | 5 |
| 1 | x | 1 | = | 1 |
| 2 | 5 | 10 |
| 3 | x | 7 | = | 21 | = | 7 |
| 4 | 18 | 72 | 24 |
| 3 | x | 4 | = | 12 | = | 1 | 1 |
| 2 | 5 | 10 | 5 |
Dividing Fractions
Division with fractions is very similar to multiplying with fractions.
| 12 divided by 12 = 1 | 12 goes into 12 once |
| 12 divided by 6 = 2 | 6 goes into 12 twice |
| 12 divided by 4 = 3 | 4 goes into 12 three times |
| 12 divided by 3 = 4 | 3 goes into 12 four times |
| 12 divided by 2 = 6 | 2 goes into 12 six times |
| 12 divided by 1 = 12 | 1 goes into 12 twelve times |
| 12 divided by 1/2 = 24 | 1/2 goes into 12 twenty four times |
This is logical when you think about the statement on the right. Whenever you are dividing by a fraction you have to multiply one fraction by the reciprocal of the other. That is, when you divide one fraction by another, you have to multiply one fraction by the inverse of the other. For example:
| 1 | divided by | 6 | = | 1 | x | 7 | = | 7 |
| 2 | 7 | 2 | 6 | 12 |
| 3 | divided by | 4 | = | 3 | x | 5 | = | 15 |
| 4 | 5 | 4 | 4 | 16 |
| 1 | 3 | divided by | 4 | = | 7 | x | 5 | = | 35 | = | 2 | 3 |
| 4 | 5 | 4 | 4 | 16 | 16 |
Whenever dividing mixed fractions (1 1/2, 2 3/4 etc) you must use improper fractions (3/2, 11/4 etc).
Multiplying and Dividing Fractions Practice Tests
Work through the following tests to make sure you are comfortable with the material.